Water Quality Estimation from Regional Characteristics

Introduction

The Clean Water Act (CWA) of 1972 and its subsequent amendments established the national goal "that the discharge of pollutants into the navigable waters be eliminated by 1985." Recently, efforts to eliminate water pollution have gained new momentum due to lawsuits against several states and the USEPA alleging failure to comply with the relatively obscure Total Maximum Daily Load (TMDL) portion of the CWA (Section 303d). This part of the act deals specifically with agriculture and other so-called "nonpoint sources" of pollution and is expected to cost the states over $2.5 billion to implement over the next few years. While the State of Utah has not been involved in any TMDL lawsuits so far, the State of Idaho is currently under court order to complete TMDL requirements that could cost over $45 million within the next 5 years. This projected expenditure is far in excess of the state’s annual budget for the entire Department of Environmental Quality is only $3.3 million. A major part of the projected expenditure for the development of TMDLs is associated with the collection and laboratory analysis of water quality samples from streams. The goal of this research project was to test a "regional analysis" method for estimating pollutant loads in stream segments where not water quality samples have been taken. 

The Total Maximum Daily Load or TMDL for a particular contaminant in a river reach is a regulatory prescription that limits pollutant concentrations to an estimate of the amount of pollution the water is capable of assimilating while maintaining its intended beneficial uses. "Pollutants" addressed by TMDLs include industrial chemicals, pesticides, fertilizers and changes in stream sediment, temperature, habitat and flow. Beneficial uses of a water body are established in state legislation and identify the level of "clean" that is needed for each stream given its intended use. These uses might include different types of fisheries, irrigation, drinking water and so forth. The process of setting TMDLs for a stream requires estimates of the natural variability of the pollution in the stream; the factors responsible for the natural and man-caused variations; the assimilative capacity of the stream for the particular pollutant; the toxicity of the pollutant to the habitat; and the frequency and duration of acceptable exceedances of safe levels. These estimates can require large amounts of at-site data which is usually not available where it is needed.

Scope

Data Used

Acquisition of data

As the goal of the project was to test the predictive capabilities of readily available data, I only used data sources that are available directly through the Internet, or are publicly available through an telephone request system.  The two main data sets used in the model include:

1) Water quality data were acquired from the USEPA STORET database.  This is a very large database of water quality observations taken by an assortment of local, state and federal agencies, and maintained by the USEPA.  At present, the STORET system involves the making of a request for data by telephone, and the transfer of that data to the users computer by FTP.  In the Internet-era, this is a bit archaic approach to acquiring data, but is still rather fast.  Because of this, it was considered that this data source can be assumed to be "readily available" and thereby be appropriate to use in the model.  Because it is collected by an assortment of agencies, the data is prone to suspicion for accuracy.  This understanding was used as partial justification for dropping a few data points which appeared as outliers having a major effect on the model accuracy. 

Aside from the telephone request system, another source of STORET data was identified in the EPA BASINS data set.  BASINS is an ArcView GIS based modeling environment developed by the USEPA Office of Science and Technology to support the development of TMDLs.  The STORET data contained in the BASINS data set for any given watershed exists in two forms.  This includes a) summary STORET data (means, number of observations and quantiles) for all stations in the region and b) raw water quality data at selected sites.  For this project, values of mean total phosphorous were extracted from the STORET data base for each selected control point in the region.  

2)  Regional attribute data were all taken directly from the EPA BASINS data set for Idaho.  The decision to use only data included in the EPA BASINS data set was made because this is a data set that is readily available to any one in the country at nearly every location throughout the country.  The data are available for download by USGS hydrologic unit boundaries, or are available delivered on a free CD from EPA by EPA region.  I chose to work exclusively with this data not because it was easy for me to acquire, but because, if the methodology being tested worked on this data, then it would be possible for anyone to do it (all having easy access to the requisite data.)

For each of the control points defined based on availability of water quality data, a set of physical characteristics were extracted from the GIS coverages.  These data included land use distribution, elevation, total area and number of reaches contributing to the control point. The land use distribution was defined within a 200 meter wide buffer strip along side the reaches upstream of the control point. 

Table 1 contains a sample of the data that was generated and used in the model development:

Selection of Control Points

The BASINS GIS database contains a coverage of water quality monitoring stations that consists of locations at which water quality data has been measured. Since the parameter of interest in this study is total phosphorous, a subset of this coverage was constructed that contains only the water quality monitoring stations at which a reasonable number of measurements (n >10) of total phosphorous exist. These stations were used as the control points for this study.

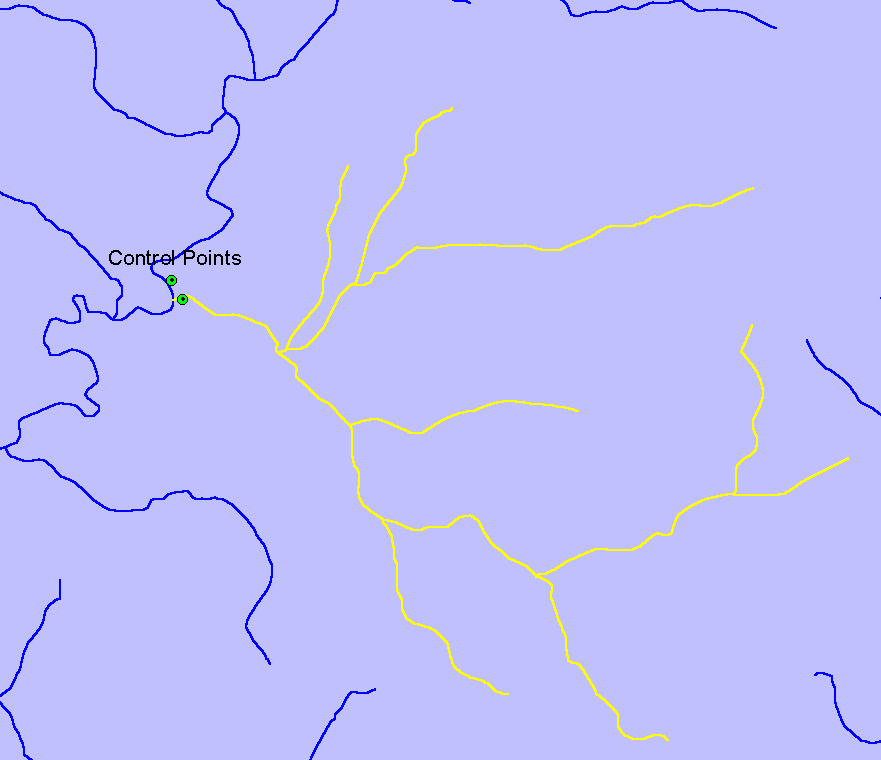
Once this coverage of total phosphorous stations was constructed an analysis was conducted to determine whether all of the stream reaches upstream of each control point could be isolated. If it was possible to select all of the upstream reaches, the control point was included in the study. If the upstream reaches were too complicated to isolate or the reach data was incomplete upstream of the control point, the point was left out of the study. It should be noted that the selected watersheds contain mostly low order streams that could be easily isolated. Figure 1 shows an example control point and its associated upstream reaches. This process was repeated until a sufficient number of control points and data were collected for regression analysis. This partial regional data set covers a geographic area that includes a large portion of southeastern Idaho.

Figure 1. Sample control-point and selected upstream reaches.

Generation of Land Use Distribution Data

Once all of the stream reaches upstream of the control point had been selected, a 100-meter buffer was drawn around all of the selected stream reaches. The 100-meter buffer was used to clip the land use data to produce a land use buffer that describes the land use for a distance of 100 meters on either side of the streams. This technique eliminated the need to go through the complicated process of delineating a sub-watershed boundary for the selected stream reaches and then characterizing the land use distribution in the entire contributing area for the control point (sub-watershed). This simplification was performed based on the assumption that only the land use within 100 meters of the stream really contributes to the concentration of total phosphorous in the stream. In other words, it is assumed that the distribution of land use in the 100-meter buffer around the stream is adequate to describe the relationship between land use and total phosphorous concentrations in the stream at the control point.

Once the land use buffer had been created, the area in each land use within the buffer was divided by the total area in the buffer to get the percentage distribution for each land use within the buffer. The resulting percentage distribution for each land use within the buffers strongly indicated that agriculture, rangeland, and forestland were the dominant land uses for the data set we considered. Very few, if any, of the control points selected had any other significant land use categories other than these three. For this reason, agriculture, rangeland, and forestland were selected as the three land use categories for regression analysis. Figure 2 shows the land use buffer associated with the selected stream reaches shown in Figure 1.

Figure 2. Land use buffer used to calculate percent distribution of land use.

Elevation Data

The BASINS software also contains coverage of elevations for the geographic area that we used in this regional analysis. This coverage was used to pick off the elevation of each of the control points, and the extracted elevation data was added to the land use distribution data. The elevation of each of the control points was added in an attempt to capture some of the variation in total phosphorous that may be attributed to differences in the other variables caused by elevation. For example, agriculture and rangeland at an elevation of 1000 meters is most likely very different than the agriculture and rangeland that could be found at an elevation of 2000 meters. The land use data that was used does not make any distinctions between the types of agriculture or rangeland that may exist in each of these general categories.

Results and Conclusion

Once the data set was developed using GIS tools, the GIS aspect of the project was complete.  The remainder of the project involved the use of the resulting table of data to build a predictive model.  As this is primarily a GIS report, I will give only a summary of what was done in the model development phase of the project.  First, the decision was made to drop all but three of the landuse categories as predictors.  This is becuase the dropped landuses were not present in many of the subwatersheds (e.g. "tundra").  The landuses which were included in the model development were forest, agriculture and rangeland (as described previously).  In addition to these predictors, total area and elevation were also allowed to enter the model.  The statistical package, S-Plus was used to develop and test linear models using these predictors and mean total phosphorous as the predictee.  A series of models were developed in S-Plus and were compared using analysis of variance (ANOVA) and by examining the R^2 value of each model fit.  The result of this activity was a series of multiple regression models, the best of which is a model based on the log transform of the mean total phosphorous data and untransformed predictors with five outlier data points removed.  This model had an R^2 fit of 0.826 and takes the following form:

log(MEANTP) = -7.95 + . 0.218 * Agriculture + 0.109 * Rangeland - 0.011 * Forest + 0.001 * Agriculture * Rangeland - 0.008 * Agriculture * Forest + 0.002 * Rangeland * Forest

The model produced from untransformed data does not fit the data very well. This is reflected by the poor R^2 (0.399) value obtained in this model run. It appears from a plot that the model does a much better job at predicting small values of total phosphorous than it does larger values of total phosphorous. This information indicated that a transformation of the data may be helpful. The second and third transformations showed similar results - the fit is better but there is still a large amount of spread.  Removing the five extreme values (as mentioned above) decreased the spread and improved the fit

Regression results showed that a very significant amount of the variation in the total phosphorous data can be explained using the simple linear model shown above.  Log-Transfomation of the data tended to produce better results than the untransformed data The best model appeared to be the log-transformed TP vs. untransformed variables (R2 = 0.621) Removing extreme values improved R2 to 0.826

Using this model, I tested a set of data that was not used in the model development. Results on this test data set ranged from an R^2 of 0.35 to 0.661 depending on whether the complete model (including very small terms) was used, or just the model shown above, as well as whether or not the model using the five outliers was used or not.  The reason that the model did not fit the prediction set as well as the fitting set is likely due to the fact that the uncertainty about the test set was greater than that about the fit set because the test set were all based on fewer than 10 measurements, while the fit set were sites with greater than 10 measurements.

Based on the relative magnitudes of the coefficients in the best model it is evident that the most important variables are percent agriculture, percent forest, percent rangeland, elevation, the combined effect of percent agriculture and percent rangeland, and percent agriculture and percent forest (elevation was not important). Additional predictees (soil type, geology, average precipitation, etc.) may improve the predictive power of the model by explaining more of the total variation in the total phosphorous data.  Give these model results, it is clear that a regional predictor model for water quality may be a very practical tool.  The use of these additional predictors, and a better experimental design will likely facilitate a clearer argument for such a model.