Prediction of Channel Geometry from DEM-Derived Channel Slope

Jason Thompson

CEE 6440 GIS in Water Resources

Introduction

Objectives

Manning's Equation

Channel Slope Determination

Channel Geometry Predictions

Channel Geometry Comparisons

Conclusions

References

Appendix

Introduction

The Santa Clara River is located in Washington County in Southwest Utah, and serves as a major tributary to the Virgin River (see Figure 1 in Appendix). The Santa Clara River is an important source of irrigation water for surrounding ranches and farms. In order to use this water for irrigation, numerous diversion structures have been built in the river. The Santa Clara also provides important habitat for the Virgin spinedace (Lepidomeda mollispinis mollispinis), which is found only in the Virgin River Basin. Because of population declines due to habitat loss and degradation, the Virgin spinedace is recognized as endangered by the state of Utah. This particular study focused on the Santa Clara below Gunlock Reservoir (see Figure 2 in Appendix). The river below the reservoir is about 37 km long, and flow in this reach is regulated by releases from Gunlock Dam.

Objectives

This study had three primary objectives. The first objective was to use tools available in ArcMap to derive channel slope for the Santa Clara below Gunlock Reservoir from a digital elevation model (DEM). The second objective was to use the DEM-derived channel slope to predict Santa Clara channel geometry. In order to accomplish this objective, Manning’s Equation was used. This equation provides a quantitative relationship between channel geometry and channel slope. The final objective was to compare the predicted channel geometry with values of channel geometry measured in the field. Channel geometry is of interest because it is useful for predictions of habitat availability for aquatic species, for estimating channel flow capacity for flood assessments, for classifying stream habitats, for sediment erosion and deposition studies, and for various channel impact analyses. If channel geometry can be accurately predicted without requiring extensive field work, then tasks such as those mentioned above could likely be done faster and less expensively.

Manning’s Equation

Channel slope and channel geometry are related through Manning’s Equation. This equation is a widely used empirical equation used for estimating discharge from channel characteristics. Manning’s Equation is given below:

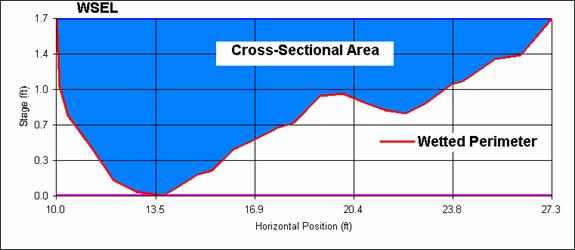
In this equation, Q is equal to the discharge (cfs); C_u is a conversion factor equal to 1.486 when using ES units; n is the Manning’s roughness factor; A is the wetted cross-sectional area (ft²); R_h is the hydraulic radius (ft), equal to the wetted cross-sectional area divided by the wetted perimeter; and S₀ is equal to the energy slope, or for uniform flow S₀ can be approximated by the slope of the channel bottom. For the purposes of this study, channel geometry is represented by the term AR_h^2/3 in Manning’s Equation. This term is equivalent to the cross-sectional area raised to the 5/3 power divided by the wetted perimeter raised to the 2/3 power. Wetted perimeter is the length of the channel in cross-section view in contact with the water in the channel. The geometry features of interest are depicted in Figure 3. According to Manning’s Equation, the calculation of channel geometry requires the discharge (Q), Manning’s roughness (n), and the channel slope (S₀):

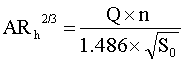
Figure 3. Description of channel geometry

Determination of Channel Slope

In order to predict channel geometry, the slope of the channel must be calculated. Assuming this value has not been measured in the field, some other means of obtaining this value would need to be identified. The possibility exists of using slope derived from a DEM for such a purpose. However, it is obvious that a DEM with a cell size of 900-m² could not be used for effectively calculating channel slope except for the case of a very large river. While it may not be feasible to estimate channel slope for smaller streams, it is still possible to accurately estimate valley slope. Valley slope refers to the slope of the valley in which the stream flows. Because valleys are larger features than channels, their slope should be able to be predicted from a 30-m DEM. 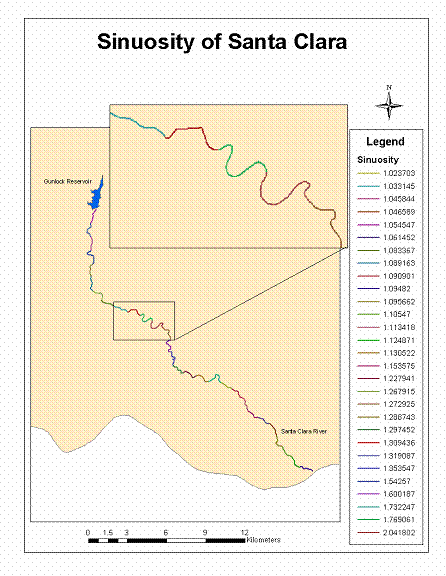Channel slope can be related to valley slope through channel sinuosity. Channel sinuosity is defined as the ratio of the length of the stream to the length of the valley. Sinuosity can also be described as the ratio of the valley slope to the channel slope (Rosgen 1994). Based on these relationships, the following equation can be used to calculate the channel slope:

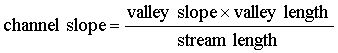
Before any of the above factors could be calculated, the hydrography data for the Upper Virgin River Watershed (HUC 15010008) was obtained from the USGS National Hydrography Dataset (http://nhd.usgs.gov/). All the data used in this study was projected in UTM Zone 12 NAD83. Then the Santa Clara below Gunlock Reservoir was subdivided into 29 segments approximately 1 km long (straight-line distance). Within each of the 29 segments, the stream length was calculated. The length of the stream within each segment was determined by the following procedure: (1) using the ArcMap Editor, a polygon was constructed of a size adequate to encompass the segment; (2) the stream within the polygon was clipped using the GeoProcessing Wizard in ArcMap with the polygon as the clip layer; (3) the clipped layer (stream) was saved as a Feature Class into a Feature Dataset within a Geodatabase in ArcCatalog. During the save and import process into the Geodatabase, the length of the clipped stream reach was automatically calculated. This process was repeated for all the 29 segments. Once a length value was determined for each of the stream reaches, then each length associated with its corresponding reach was added into the attribute table for that reach. All of the reaches were then merged together using the GeoProcessing Wizard. The result was the Santa Clara below Gunlock Reservoir, subdivided into reaches, with a length attribute associated with each reach. Figure 4 (in Appendix) visually demonstrates the components needed for the calculation of stream length, including the constructed polygons and the distinct stream reaches associated with each segment.

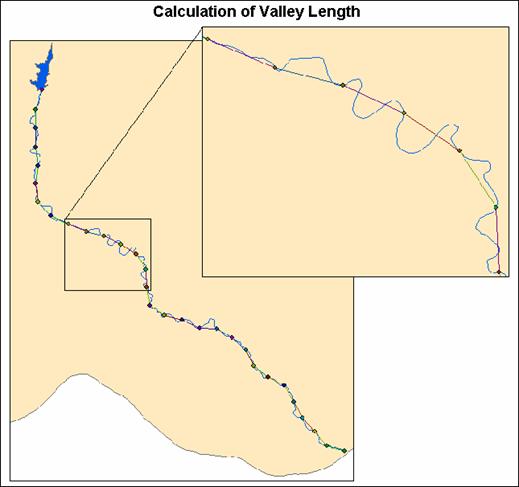
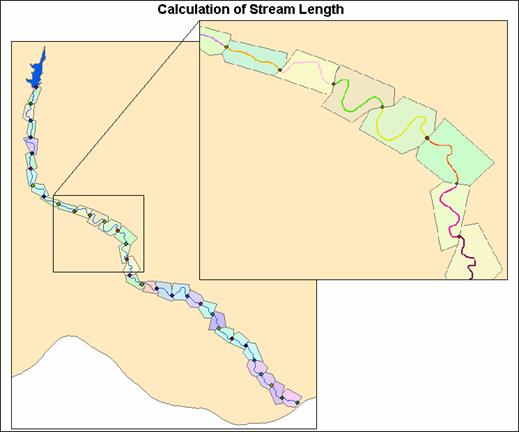
The valley length for each segment was assumed to be equivalent to the straight-line length of each segment. This approximation is often made when calculating sinuosity. The length of each segment was calculated using the following procedure: (1) a line Feature Class was created in a Feature Dataset in ArcCatalog; (2) the line Feature Class was added into ArcMap, and the line was constructed along the length of a segment using the ArcMap Editor; (3) upon completion of the editing, the length of the line was automatically calculated. This procedure was repeated for all 29 segments. Each line length was then added into the attribute table of its corresponding segment. Figure 5 (in Appendix) shows each of the distinct lines created along the length of each segment for the Santa Clara below the reservoir.

Once values of stream length and valley length were calculated for each segment, then the sinuosity of each segment was easily calculated. These calculations were performed in Excel. Once these calculations were done, the sinuosity values for each segment were added to the appropriate segment attribute table. 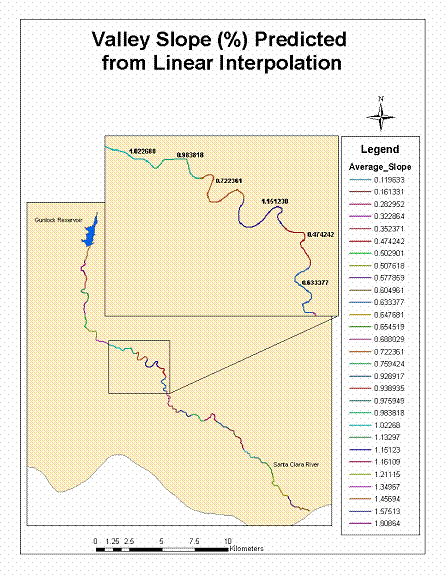The segments were merged together and a map was produced showing sinuosity values associated with 1-km segments of the Santa Clara. This map is presented in Figure 6 (in Appendix).

The final component required for the calculation of the channel slope was the valley slope. The first step was the calculation of slope (%) in a raster format (grid cell size of 900-m²) from a DEM using Spatial Analyst in ArcMap. The 30-m DEM was obtained from the USGS National Elevation Dataset (http://edcnts12.cr.usgs.gov/ned/default.htm). Before the slope calculation, the pits in the DEM were filled using TauDEM. Three different approaches were used for the estimation of valley slope. Different approaches were used in order to compare varying methodologies in an attempt to identify the most useful approach and evaluate the resulting values for valley slope. The first approach was to estimate valley slope as simply elevation change divided by the change in distance for each segment. Elevations were obtained directly from the DEM at the beginning and end points of each segment using the identify tool in ArcMap. Because the distance between those segment endpoints was previously determined, the slope could be calculated along the segment. This method was referred to as the linear slope method, and provided a simple means of estimating valley slope. The values of slope were then added to the attribute table for each segment. Figure 7 (in Appendix) shows the slope values for each stream segment obtained using this method.

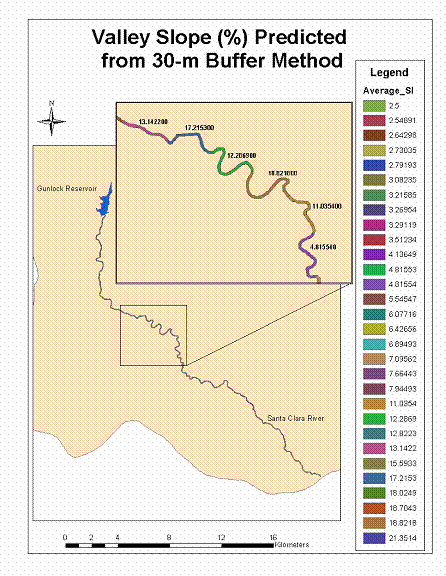
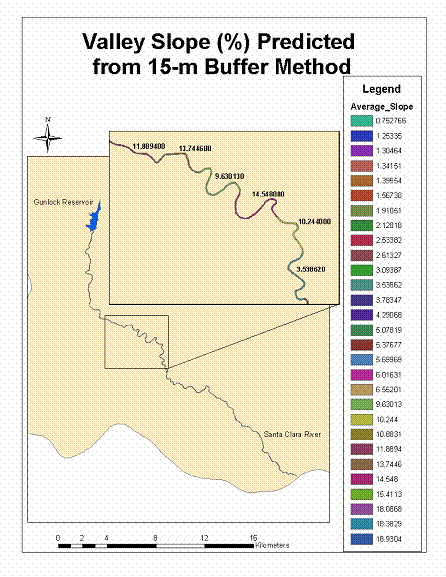
The second approach used for estimating valley slope involved calculating the average slope within a buffer established around the stream. This approach was chosen because it was initially thought that the slope within the stream buffer would provide an adequate representation of the stream valley slope. While the first approach approximated slope based on elevation values about 1 km apart, this approach estimated average slope based on numerous slope values in an area adjacent to the stream. Initially, the ArcMap Buffer Wizard was used to construct a 30-m buffer around the Santa Clara. A 30-m buffer was chosen because of the cell size of the slope raster. The next step was to convert the slope raster to a shapefile. However, before that could be done, the raster floating-point values had to be reclassified as integer values using the Reclassify Tool in Spatial Analyst. With this tool, a range of floating-point slope values was manually reclassified such that the low and high values in each range were separated by a value of 1(%). Then, this range of slope values was reclassified as an integer, where the integer value was equal to the mean of the range of values. For example, the first range of slope values was assigned as 0-1%, and the integer value for this range was assigned as 0.5%. This technique of classification was deemed an efficient, yet accurate means of assigning slope values. Once this was accomplished, then the slope raster was converted to a shapefile. Then this slope shapefile was clipped using the GeoProcessing Wizard, with the 30-m buffer layer serving as the clip layer. The results were saved in a Feature Dataset as a Feature Class. The shapefile produced by the first clip was then divided into the 29 segments from before by clipping with the previously constructed polygons. By saving the first clip as a Feature Class, each slope value had a calculated area associated with it based on the grid cell size, allowing for the calculation of an area-weighted slope. Both clips allowed for the average area-weighted slope to be calculated within each buffer for each segment. These results are presented in Figure 8 (in Appendix). The final approach for estimating valley slope was identical to the second approach, except that a 15-m buffer was used rather than a 30-m buffer. Two different sized buffers were used in order to examine the relationship between buffer size and the resulting valley slope. The slope results from the 15-m buffer method are presented in Figure 9 (in Appendix).

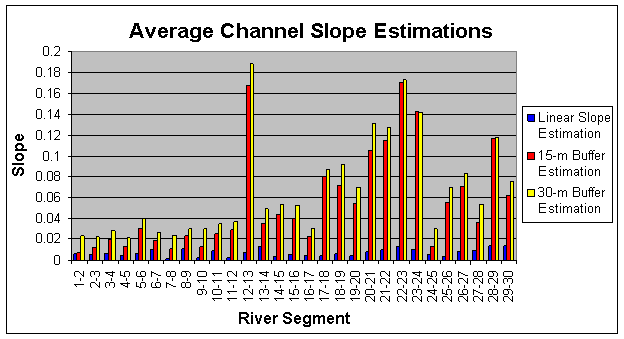
The channel slopes resulting from the linear slope, 30-m buffer, and 15-m buffer estimation methods are presented graphically in Figure 10 below. This chart shows that the two buffer methods predicted fairly similar channel slopes, but greater values than the linear slope method. There does not appear to be a distinct trend between slope and segment location with the linear slope method. With the two buffer methods, there does appear to be a general trend of increasing slope with segment location upstream to segment 22-23.

Besides calculating channel slope from valley slope using sinuosity, channel slope was also estimated directly from the slope raster produced from the DEM using Spatial Analyst. The identify tool in ArcMap was used to determine slope values at several locations on the Santa Clara where cross-sections were established during the Summer of 2001. These locations were known because the cross-sections were located with GPS. The slope obtained at each of these locations was assumed to be representative of the slope of the channel at that location. This method was examined in an attempt to identify a simple way to estimate channel slope from a slope raster. This technique is subsequently referred to as the point slope prediction method.

Figure 10. Estimations of channel slope from three methods

Predictions of Channel Geometry

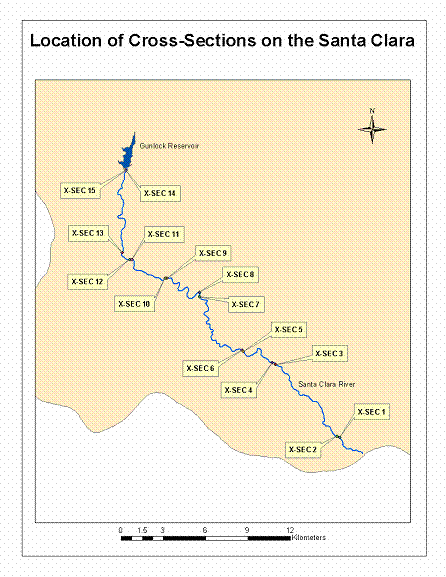
As mentioned above, cross-sections were established on the Santa Clara below Gunlock Reservoir as part of a flow study during the Summer of 2001. A total of 15 cross-sections were established, and at each cross-section discharge and channel topography were measured. Channel topography was surveyed as distance-elevation pairs along a measuring tape stretched across each cross-section. The location of each of the cross-sections is presented in Figure 11 (in Appendix). Manning’s Equation was used to predict channel geometry (AR_h^2/3) at each of these cross-sections. When using Manning’s Equation, discharge is one of the parameters required. The discharge used was the discharge measured at each of these cross-sections. Another parameter required is Manning’s roughness factor, n. This factor was estimated based on a formula proposed by Cowan (1956). This formula takes into account known channel characteristics, including bed substrate size, in-channel vegetation, channel sinuosity, and other factors contributing to roughness. Table 1 contains the estimated Manning’s roughness factors for each of the cross-sections. In this table,

n = (n_b + n₁ + n₂ + n₃ + n₄)m, where n_b is the base value of n, n₁ is a correction for surface irregularities, n₂ is a correction for cross-section size and shape, n₃ is a correction for obstructions, n₄ is a correction for vegetation, and m is a correction for channel meandering. The final parameter required is channel slope, which was estimated using the four different methods discussed above. 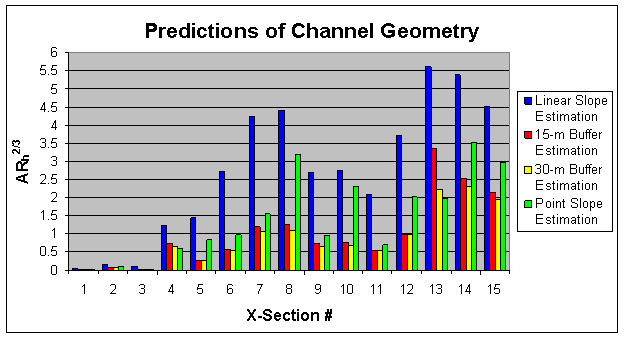The results of the channel geometry calculations are presented in Figure 12 below.

Table 1. Manning’s roughness factor for each cross-section

X-SEC	n	n_b	n₁	n₂	n₃	n₄	m
1	0.02	0.02	0	0	0	0	1
2	0.02	0.02	0	0	0	0	1
3	0.031	0.03	0.001	0	0	0	1
4	0.031	0.03	0.001	0	0	0	1
5	0.031	0.03	0.001	0	0	0	1
6	0.031	0.03	0.001	0	0	0	1
7	0.03565	0.03	0.001	0	0	0	1.15
8	0.03565	0.03	0.001	0	0	0	1.15
9	0.031	0.03	0.001	0	0	0	1
10	0.031	0.03	0.001	0	0	0	1
11	0.03565	0.03	0.001	0	0	0	1.15
12	0.03565	0.03	0.001	0	0	0	1.15
13	0.031	0.03	0.001	0	0	0	1
14	0.031	0.03	0.001	0	0	0	1
15	0.031	0.03	0.001	0	0	0	1

Figure 12. Channel geometry predictions for each cross-section

Figure 12 shows that in general, the linear slope method predicted the highest values of channel geometry for each cross-section, followed by the point slope method. The two buffer methods typically predicted the lowest values. With all four methods, channel geometry values were relatively small for the first three cross-sections with an increase between cross-sections 4 and 8. Each of the methods, with the exception of the point slope method, predicted fairly similar geometry values for cross-sections 9 through 12, but differences existed between the methods. For the linear slope method and the two buffer methods, the highest geometry values predicted for all the cross-sections occurred for cross-sections 13 through 15. The point slope method was more variable.

Comparing Predicted and Measured Channel Geometry

The final objective of this study was to compare the predicted values of channel geometry with the values measured at each of the cross-sections. As stated previously, distance-elevation data were surveyed along each cross-section. However, this data needed to be converted to the form of channel geometry used in this study (AR_h^2/3). In order to derive cross-sectional area and hydraulic radius from the survey data, the program WinXSPRO, developed by the USDA Forest Service, was used. One of the operations available with WinXSPRO is the conversion of distance-elevation pairs into channel cross-sectional area and wetted perimeter, from which the hydraulic radius can be calculated. 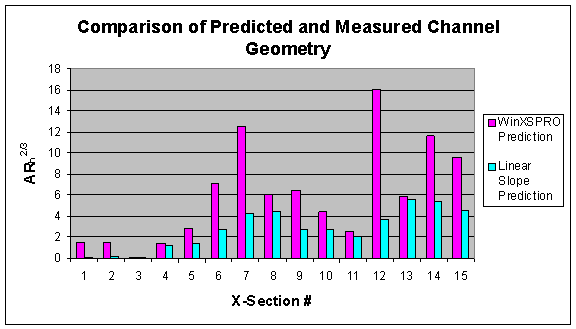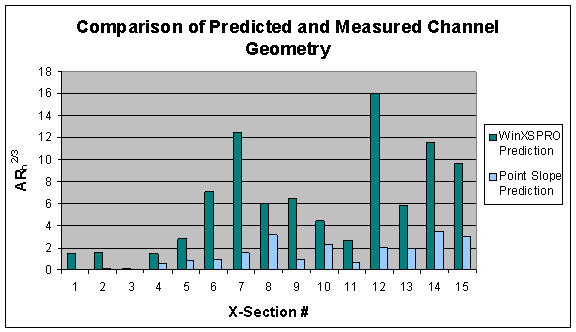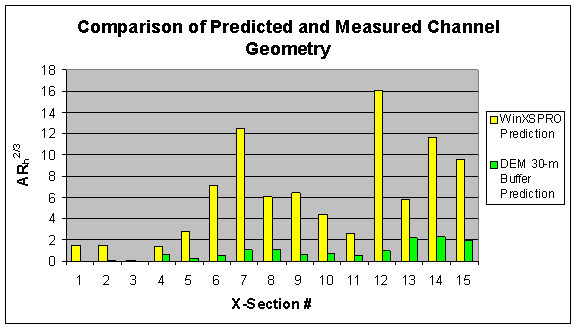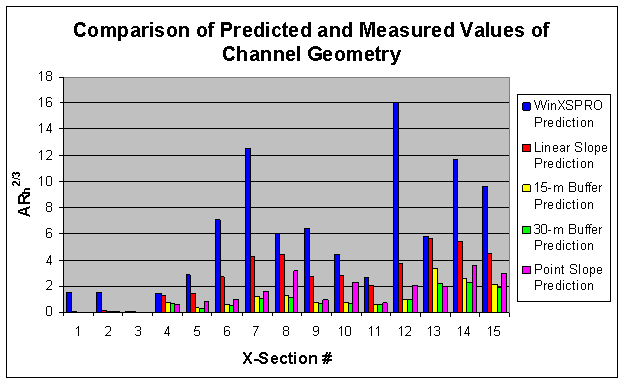Figures 13, 14, 15, and 16 (in Appendix) compare the measured channel geometry values with those predicted by the linear slope, point slope, 30-m buffer, and 15-m buffer methods, respectively. Figure 17 below summarizes the predicted and measured geometry values. This figure shows that in general, the measured geometry values were much greater than the predicted values. Of the four prediction methods, the linear slope method produced geometry results most similar to the measured values, followed by the point slope method. The two buffer methods did not predict geometry well relative to the measured values. 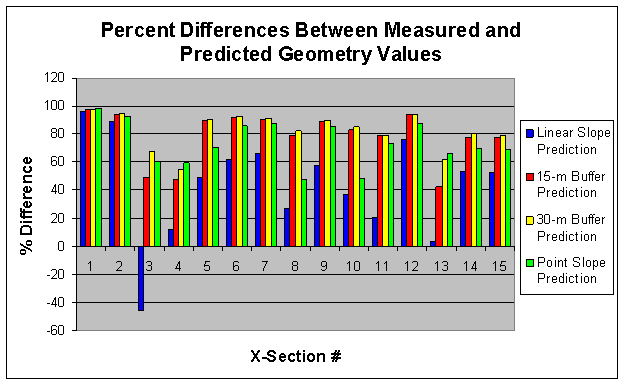Figure 18 below shows the differences in percent between the measured and predicted geometry values. The information in this figure reaffirms the above observation that the linear slope method produced results most similar to the measured values. The two buffer methods produced very similar results, with the 15-m buffer method predicting only slightly better in general. This result indicates that changing the buffer size from 30-m to 15-m did not markedly improve the prediction power of the buffer method. It is interesting to note from Figure 17 that although the linear slope method predicted lower geometry values than those measured, there appears to be a similar trend between the values. In a further attempt to investigate data trends, Figure 19 was produced. In this figure, the multiplicative factor on the y-axis was obtained by simply dividing the measured geometry value by the predicted value for each of the methods. The differences in Figure 19 between the measured and predicted values are initially very high for all four methods but then tend to decrease with upstream cross-section. As expected, both buffer methods exhibit very similar trends in this figure. The point slope method displays a similar trend to the buffer methods, but in a less pronounced, more dampened manner. This figure also shows that the linear slope method and the measured values do exhibit a similar trend, particularly upstream of and including cross-section 3. At these cross-sections, the multiplicative factor maintains a fairly constant value, indicating a relatively uniform relationship. The relationship between the other methods’ predictions and the measured values appears to be much more variable.

Figure 17. Geometry summary comparison

Figure 18. Differences (%) between measured and predicted geometry

Figure 19. Differences between measured and predicted geometry

Conclusions

Based on the above study, several conclusions can be drawn regarding the applicability of predicting channel geometry from Manning’s Equation, with the channel slope in the aforementioned equation derived from a DEM. In this particular study, none of the four techniques used for estimating channel slope consistently produced channel geometry values similar to the values measured at each cross-section. Of the techniques used, the linear slope method predicted geometry most accurately relative to the measured values. Geometry values predicted by the linear slope method and the measured values also exhibited a very similar trend based on cross-section location. Using slope values directly from the slope raster at each cross-section location did not prove to be a reliable method for estimating channel slope at that location. Both the 30-m and the 15-m buffer methods predicted similar geometry values, but underestimated geometry relative to the measured values. The inaccuracy of these buffer methods was most likely due to the topography characteristics adjacent to the Santa Clara in the study area. In this area, there is major slope variability and steep slopes in close proximity to the stream, leading to an overestimation of valley slope with the buffer methods. The DEM used in this study, with a cell size of 900-m², appears to be too coarse for deriving valley and channel slope for a small stream in widely-varying topography like the Santa Clara. A more detailed DEM, like one with a cell size of 100-m², might dramatically increase the similarities between predicted and measured geometry values. Also, the buffer method approach would probably predict results more comparable to measured values for a larger stream with a wider floodplain and surrounded by less extreme topography variations. It is also possible that a better equation than Manning’s Equation could be used relating channel geometry and channel slope. Manning’s Equation is a relatively simple equation, and is dependent on a roughness factor that is often difficult to adequately quantify. If an empirical equation relating geometry and channel slope could be developed for a specific stream of interest, then the ability to accurately predict channel geometry would likely be greatly improved.